Irrigation Design Tip: Calculating Precipitation Rates
The precipitation rate of the sprinklers you have selected for the project should be calculated to determine first if the rate exceeds the soil’s intake rate (which it shouldn’t) and, secondly, if the rate will apply enough water during acceptable operating times to meet the irrigation requirement (which it should).
The average precipitation rate is expressed in inches per hour (millimeters per hour).
A simple formula is used to calculate precipitation rates for sprinklers using the area inside the sprinkler spacing and the gallons per minute (cubic meters per hour) being applied to that area.
The formula looks like this:

| US Measurements | Metric |
| PR = the average precipitation rate in inches per hour | PR = the average precipitation rate in millimeters per hour |
| 96.3 = a constant which incorporates inches per square foot per hour | 1000 = a constant which converts meters to millimeters |
| gpm = the total gpm applied to the area by the sprinklers | m3/h = the total m3/h applied to the area by the sprinklers |
| S = the spacing between sprinklers | |
| L = the spacing between rows of sprinklers | |
The constant of 96.3 (1,000) is derived as follows:
1 gal water = 231 in3 1 ft2 = 144 in2
(1000 mm = 1 m)
Question: If one gallon of water was applied to 1 ft2 how deep in inches would the water be?
231 in3/gal = 1.604 inches deep
144 in2/ft2
One of the multipliers in the upper half of the equation is the gallons per minute applied by the sprinklers. To convert this to gallons per hour we need to multiply by 60 minutes. To work this into the constant, we multiply 1.604 in x 60 min and we come up with the 96.3 for the formula. (In the International System Units version of the formula, because the multipliers already are in meters cubed per hour, you do not need to convert the 1000 before using it in the formula.)
Example for Four Full Circle Impact Sprinklers
Let’s look at an example of a precipitation rate calculation for four full circle impact sprinklers. Each sprinkler has a radius of throw of 40 ft (12 m) at 40 psi (3 bar), a discharge of 4.4 gpm (1 m3/h) and the sprinklers are spaced at 40 ft (12 m) square spacing.
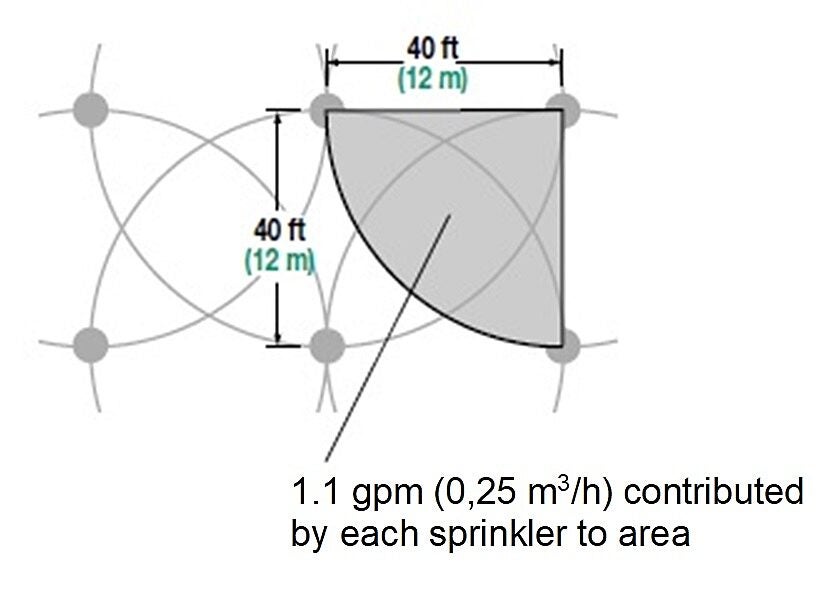
Each full circle sprinkler delivers only 1/4 of its flow into the area between the four sprinklers. The other 3/4 of each sprinkler’s rotation pattern is outside the area. With 4.4 gpm (1 m3/h) total per sprinkler, only 1.1 gpm (0,25 m3/h) is delivered per sprinkler into the area between them. When four sprinklers delivering 1.1 gpm (0,25 m3/h) each are added together, they are the equivalent of one full circle sprinkler or 4.4 gpm (1 m3/h). With full circle sprinklers, you can use the equivalent of one sprinkler’s discharge as the gallons per minute (meters cubed per hour) for the precipitation rate formula.
The formula for this example would be

The above calculation tells you that the sprinklers at that spacing, if given the pressure required, will apply water at slightly more than 1/4 in (6,9 mm) per hour.
Example for Four Half Circle Impact Sprinklers
Using the same 40 ft x 40 ft (12 m x 12 m) spacing that we used earlier, let’s look at those same sprinklers in half circle configuration.
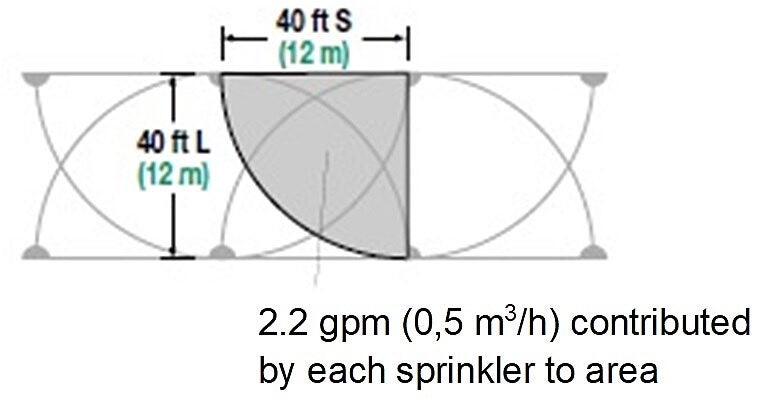
With the same performance specs of 4.4 gpm (1 m3/h) per sprinkler and all the sprinklers now set at half circle, the formula is:

Even though there are eight sprinklers in the diagram, we are only interested in the area between four adjacent sprinklers. The 8.8 gal (2 m3/h) was determined by adding up the part of the discharge from each sprinkler that it contributed to the area. With each sprinkler in the half circle setting, one half of its flow was distributed into the square pattern while the other half went into the neighboring pattern. The amount of flow per sprinkler, then, was 2.2 gpm (0,5 m3/h) multiplied by four sprinklers for a total of 8.8 gpm (2 m3/h).
Example for Four Sprinklers (Corner)
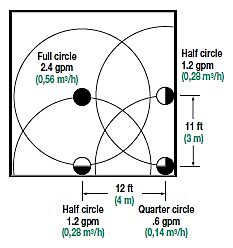
Spray sprinklers have fixed arcs of coverage and some have matched precipitation rates. Let’s look at a PR calculation for four spray sprinklers in the corner of a lawn area with these statistics:
| Spacing | S = 11 ft (3 m), L = 12 ft (4 m) |
| Operating psi at sprinkler | 25 psi (1,7 bar) |
| Radius of throw | 11 ft (3 m), regardless of pattern |
| Discharge | |
| Full circle | 2.4 gpm (0,56 m3/h) |
| Half circle | 1.2 gpm (0,28 m3/h) |
| Quarter circle | .6 gpm (0,14 m3/h) |
The spacing pattern might look like this:
The total amount of water being applied to the area by these matched precipitation rate spray sprinklers is:
| Full circle sprinkler = | 0.6 gpm (0,14 m3/h) | [1/4 of its discharge] |
| Half circle sprinkler = | 0.6 gpm (0,14 m3/h) | [1/2 of its discharge] |
| Half circle sprinkler = | 0.6 gpm (0,14 m3/h) | [1/2 of its discharge] |
| Quarter circle sprinkler = | 0.6 gpm (0,14 m3/h) | [all of its discharge] |
| Total = 2.4 gpm (0,56 m3/h) applied to the area | ||
In calculating the rate for this example, the formula would be:

You now know to expect a precipitation rate of 1.75 in/h (47 mm/h).
Calculating Triangular Sprinkler Spacing
Triangular spacing is just as easy to work with when calculating the precipitation rate as square or rectangular spacing. The main difference is calculating the height of the pattern before using it as one of the dimensions in the formula.
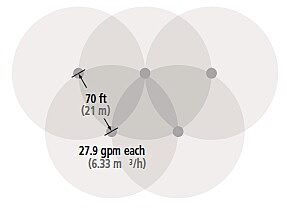
In this example, large size rotors are spaced head-to-head at 70 ft (21 m) in a triangular pattern. The gallons per minute (meters cubed per second) from each of these full circle sprinklers is 27.9 (6,33 m3/h).
The pattern would look like this:
A good example for the use of the sliding pattern method is the sprinkler spacing often designed for the outfield of a baseball field. The designer may start with rectangular spacing behind third base and, while following the outside curve of the scalped area of the baselines, gradually slide through the parallelogram patterns to triangular behind second base, and continue sliding back through the patterns to rectangular again behind first base. This sliding method of spacing the sprinklers would continue right out to the part-circle sprinklers along the outfield fence.
One dimension in the spacing pattern is 70 ft (21 m), the spacing between sprinklers, and the other is the height of the pattern, the spacing between rows of sprinklers.
This height is the spacing multiplied by .866.
In this case, we have a height calculation of:
70 ft x .866 = 60.62 ft (21 m x .866 = 18,19 m)
The dimensions to use in the PR formula for this situation are 70 ft x 60.62 ft (21 m x 18,19 m).
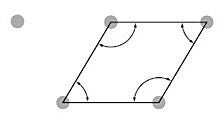 The easiest way to calculate the PR for triangular patterns is to treat them as parallelograms, using four sprinklers instead of three. When examining the pattern as a parallelogram, you can see that two of the sprinklers are contributing less of an arc (and therefore a smaller part of their flow to the area) than the other two. The other two, however, contribute proportionally larger flows so that the total flow matches that of four sprinklers in a rectangular pattern.
The easiest way to calculate the PR for triangular patterns is to treat them as parallelograms, using four sprinklers instead of three. When examining the pattern as a parallelogram, you can see that two of the sprinklers are contributing less of an arc (and therefore a smaller part of their flow to the area) than the other two. The other two, however, contribute proportionally larger flows so that the total flow matches that of four sprinklers in a rectangular pattern.
The PR calculation for this example would be:

Now that you have been exposed to calculating precipitation rates, you can do a few sample problems relating to the items covered in this irrigation tip. You can find exercises on page 47 of Rain Bird’s Irrigation Design Manual, then compare your answers to those in the Solutions section on page 90.
This tip was excerpted from the Irrigation Design Manual